Parameters#

Introduction#

The RAO parameters allow tuning the RAO:

to choose the business objective function of the RAO (maximize min margin, get a positive margin, …)
to activate/deactivate optional business features
to fine-tune the search algorithm, improve performance and/or quality of results

RAO parameters can be constructed using:

The Java API (see source code)
A JSON file (see example)
A PowSyBl configuration file (see example)

Global parameters#

These parameters should be always set in the RAO parameters file or object.

Objective function parameters#

These parameters (objective-function) configure the remedial action optimisation’s objective function.

type#

Expected value: one of the following:
- “MAX_MIN_MARGIN_IN_MEGAWATT”
- “MAX_MIN_MARGIN_IN_AMPERE”
- “MAX_MIN_RELATIVE_MARGIN_IN_MEGAWATT”
- “MAX_MIN_RELATIVE_MARGIN_IN_AMPERE”
Default value: “MAX_MIN_MARGIN_IN_MEGAWATT”
Usage: this parameter sets the objective function of the RAO. For now, the existing objective function are:
- MAX_MIN_MARGIN_IN_MEGAWATT: maximization of the min(margin), where min(margin) is the smallest margin of all CNECs and the margins are considered in MW.
- MAX_MIN_MARGIN_IN_AMPERE: maximization of the min(margin), where min(margin) is the smallest margin of all CNECs and the margins are considered in A. Note that this objective function is not just a homothety of the previous one, as CNECs from different voltage levels will not have the same weight in the objective function depending on the unit considered (MW or A). This objective function only works in AC-load-flow mode (see sensitivity-parameters).
- MAX_MIN_RELATIVE_MARGIN_IN_MEGAWATT: same as MAX_MIN_MARGIN_IN_MEGAWATT, but the margins will be relative (divided by the absolute sum of PTDFs) when they are positive.
- MAX_MIN_RELATIVE_MARGIN_IN_AMPERE: same as MAX_MIN_MARGIN_IN_AMPERE, but the margins will be relative (divided by the absolute sum of PTDFs) when they are positive.

forbid-cost-increase#

Expected value: true/false
Default value: false
Usage: if this parameter is set to true, OpenRAO will post-check the results after optimisation. If the value of the objective function is worse after optimisation than before optimisation, then it will return the initial solution (i.e. no PRA and no CRA applied).
This can happen for example if the preventive RAO decreases the margin on a curative CNEC, which cannot be reverted during curative RAO.
If this parameter is set to false, OpenRAO will return the real result of optimisation, which has a worse result than the initial situation.

preventive-stop-criterion#

Expected value: one of the following:
- “MIN_OBJECTIVE”
- “SECURE”
Default value: “SECURE”
Usage: Stop criterion of the preventive RAO search-tree.
- MIN_OBJECTIVE: the search-tree will maximize the minimum margin until it converges to a maximum value, or until another stop criterion has been reached (e.g. max-preventive-search-tree-depth).
- SECURE: the search-tree will stop as soon as it finds a solution where the minimum margin is positive.
  Note: if the best possible minimum margin is negative, both stop criterion will return the same solution.

curative-stop-criterion#

Expected value: one of the following:
- “MIN_OBJECTIVE”
- “SECURE”
- “PREVENTIVE_OBJECTIVE”
- “PREVENTIVE_OBJECTIVE_AND_SECURE”
Default value: “MIN_OBJECTIVE”
Usage: stop criterion for the curative RAO search-tree.
- MIN_OBJECTIVE: the search-tree will maximize the minimum margin until it converges to a maximum value, or until another stop criterion has been reached (e.g. max-curative-search-tree-depth).
- SECURE: the search-tree will stop as soon as it finds a solution where the minimum margin is positive.
- PREVENTIVE_OBJECTIVE: the search-tree will stop as soon as the preventive RAO’s objective value is reached, and improved by at least “curative-rao-min-obj-improvement”.
- PREVENTIVE_OBJECTIVE_AND_SECURE: the search-tree will stop as soon as the preventive RAO’s objective value is reached, and improved by at least “curative-rao-min-obj-improvement”, and all margins are positive.
The values “PREVENTIVE_OBJECTIVE” and “PREVENTIVE_OBJECTIVE_AND_SECURE” allow you to speed up the curative RAO without deteriorating the final solution (minimum margin over all perimeters). However, using them means the flow-based domain is not maximised for all perimeters.

curative-min-obj-improvement#

Expected value: numeric value, where the unit is that of the objective function
Default value: 0
Usage: used as a minimum improvement of the preventive RAO objective value for the curative RAO stop criterion, when it is set to PREVENTIVE_OBJECTIVE or PREVENTIVE_OBJECTIVE_AND_SECURE.

optimize-curative-if-preventive-unsecure#

Expected value: true/false
Default value: false
Usage: if this parameter is set to true, OpenRAO will continue optimizing curative states even if preventive state is unsecure. If this parameter is set to false, OpenRAO will stop after preventive if preventive state is unsecure and won’t try to improve curative states.

Note: Only applied when “preventive-stop-criterion” is set to SECURE. In this case, if preventive was unsecure, second preventive won’t be run, even if curative cost is higher, in order to save computation time

Range actions optimisation parameters#

These parameters (range-actions-optimization) tune the linear optimiser used to optimise range actions.
(See Modelling CNECs and range actions)

max-mip-iterations#

Expected value: integer
Default value: 10
Usage: defines the maximum number of iterations to be executed by the iterating linear optimiser of the RAO.
One iteration of the iterating linear optimiser includes: the resolution of one linear problem (MIP), an update of the network with the optimal PST taps found in the linear problem, a security analysis of the updated network and an assessment of the objective function based on the results of the security analysis.
The linear problem relies on sensitivity coefficients to estimate the flows on each CNEC, and those estimations might not be perfect when several PSTs taps are significantly changed. When the linear optimisation problem makes a (n+1)th iteration, it refines its solution with new sensitivity coefficients, which better describe the neighbourhood of the solution found in iteration (n).
Note that the linear optimisation problems usually “converge” with very few iterations (1 to 4 iterations).

pst-model#

Expected value: one of the following:
- “CONTINUOUS”
- “APPROXIMATED_INTEGERS”
Default value: “CONTINUOUS”
Usage: the method to model PSTs in the linear problem:
- CONTINUOUS: PSTs are represented by their angle set-points; the set-points are continuous optimisation variables and OpenRAO rounds the result to the best tap (around the optimal set-point) after optimisation. This approach is not very precise but does not create integer optimisation variables; thus it is quicker to solve, especially with open-source solvers.
- APPROXIMATED_INTEGERS: a PST is represented by its tap positions, and these tap positions are considered proportional to the PST’s angle set-point (hence the “approximated” adjective). Thus, these tap positions can be used as a multiplier of the sensitivity values when representing the impact of the PST on CNECs. This approach is more precise and thus has the advantage of better respecting Loop-Flow and MNEC constraints. But it introduces integer variables (tap positions) and can be harder to solve.
  See Using integer variables for PST taps.

pst-penalty-cost#

Expected value: numeric value, unit: unit of the objective function / ° (per degree)
Default value: 0.01
Usage: the pst-penalty-cost represents the cost of changing the PST set-points, it is used within the linear optimisation problem of the RAO, where, for each PST, the following term is added to the objective function: pst-penalty-cost $$\times |\alpha - \alpha_{0}|$$*, where *$$\alpha$$* is the optimized angle of the PST, and *$$\alpha_{0}$$ the angle in its initial position.
If several solutions are equivalent (e.g. with the same min margin), a strictly positive pst penalty cost will favour the ones with the PST taps the closest to the initial situation.

pst-sensitivity-threshold#

Expected value: numeric value, unit: MW / ° (per degree)
Default value: 0.0
Usage: the pst sensitivity coefficients which are below the pst-sensitivity-threshold will be considered equal to zero by the linear optimisation problem. Filtering some small sensitivity coefficients have the two following perks for the RAO:
- it decreases the complexity of the optimisation problem by reducing significantly the number of non-zero elements
- it can avoid changes of PST set-points when they only allow to earn a few MW on the margins of some CNECs.

hvdc-penalty-cost#

Expected value: numeric value, unit: unit of the objective function / MW
Default value: 0.001
Usage: the hvdc-penalty-cost represents the cost of changing the HVDC set-points, it is used within the linear optimisation problem of the RAO, where, for each HVDC, the following term is added to the objective function: hvdc-penalty-cost x |P - P0|, where P is the optimized target power of the HVDC, and P0 the initial target power.
If several solutions are equivalent (e.g. with the same min margin), a strictly positive hvdc penalty cost will favour the ones with the HVDC set-points the closest to the initial situation.

hvdc-sensitivity-threshold#

Expected value: numeric value, unit: MW / MW
Default value: 0.0
Usage: the hvdc sensitivity coefficients which are below the hvdc-sensitivity-threshold will be considered equal to zero by the linear optimisation problem. Filtering some of the small sensitivity coefficients have the two following perks regarding the RAO:
- it decreases the complexity of the optimisation problem by reducing significantly the number of non-null elements
- it can avoid changes of HVDC set-points when they only allow to earn a few MW on the margins of some CNECs.

injection-ra-penalty-cost#

Expected value: numeric value, unit: unit of the objective function / MW
Default value: 0.001
Usage: the injection-ra-penalty-cost represents the cost of changing the injection set-points, it is used within the linear optimisation problem of the RAO, in the same way as the two types of RangeAction above.

injection-ra-sensitivity-threshold#

Expected value: numeric value, unit: MW / MW
Default value: 0.0
Usage: the injection sensitivity coefficients which are below the injection-ra-sensitivity-threshold will be considered equal to zero by the linear optimisation problem.
The perks are the same as the two parameters above.

ra-range-shrinking#

Expected value: one of the following:
- “DISABLED”
- “ENABLED”
- “ENABLED_IN_FIRST_PRAO_AND_CRAO”
Default value: “DISABLED”
Usage: CASTOR makes the approximation that range action sensitivities on CNECs are linear. However, in active+reactive computations, this approximation may be incorrect. The linear problem can thus find a worse solution than in its previous iteration.
- DISABLED: if this situation occurs, the linear problem stops and returns the previous solution, see this schema : Linear Remedial Actions Optimisation.
- ENABLED: this introduces two new behaviors to the iterating linear optimiser:
  1. If the linear problem finds a solution worse than in its previous iteration, it continues iterating.
    When stop condition is met (max-mip-iterations reached, or two successive iterations have the same optimal RA set-points), then the problem returns the best solution it has found.
  2. At each new iteration, the range action’s allowed range shrinks according to equations described here. These equations have been chosen to force the linear problem convergence while allowing the RA to go back to its initial solution if needed.
- ENABLED_IN_FIRST_PRAO_AND_CRAO: same as ENABLED but only for first preventive and curative RAO. This parameter value has been introduced because sensitivity computations in the second preventive RAO can be slow (due to the larger optimization perimeter), thus computation time loss may outweigh the gains of RA range shrinking.

linear-optimization-solver#

These are parameters that tune the solver used to solve the MIP problem.

solver#

Expected value: one of the following:
- “CBC”
- “SCIP”
- “XPRESS”
Default value: “CBC”
Usage: the solver called for optimising the linear problem.
Note that theoretically all solvers supported by OR-Tools can be called, but the OpenRAO interface only allows CBC (open-source), SCIP (commercial) and XPRESS (commercial) for the moment.
If needed, other solvers can be easily added.

relative-mip-gap#

Expected value: double
Default value: 0.0001
Usage: the relative MILP (Mixed-Integer-Linear-Programming) target gap.
During branch-and-bound algorithm (only in MILP case), the solver will stop branching when this relative gap is reached between the best found objective function and the estimated objective function best bound.

solver-specific-parameters#

Expected value: String, space-separated parameters (keys and values) understandable by OR-Tools (for example “key1 value1 key2 value2”)
Default value: empty
Usage: this can be used to set solver-specific parameters, when the OR-Tools API and its generic parameters are not enough.

Network actions optimisation parameters#

These parameters (topological-actions-optimization) tune the search-tree algorithm when searching for the best network actions.

max-preventive-search-tree-depth#

Expected value: integer
Default value: 2^32 -1 (max integer value)
Usage: maximum search-tree depth for preventive optimization.
Applies to the preventive RAO.

max-auto-search-tree-depth#

Expected value: integer
Default value: 2^32 -1 (max integer value)
Usage: maximum search-tree depth for the optimization of available auto network actions.

max-curative-search-tree-depth#

Expected value: integer
Default value: 2^32 -1 (max integer value)
Usage: maximum search-tree depth for curative optimization.
Applies separately to each perimeter-specific curative RAO.

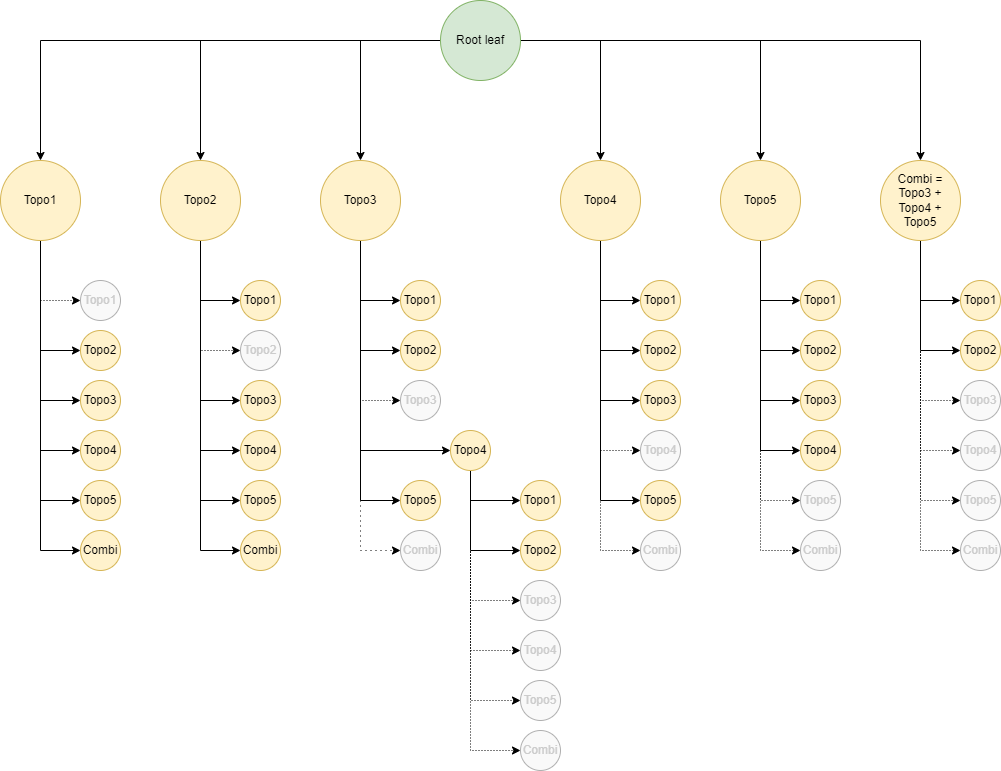
predefined-combinations#

Expected value: an array containing sets of network action IDs
Default value: empty
Usage: this parameter contains hints for the search-tree RAO, consisting of combinations of multiple network actions that the user considers interesting to test together during the RAO.
These combinations will be tested in the first search depth of the search-tree

absolute-minimum-impact-threshold#

Expected value: numeric value, where the unit is that of the objective function
Default value: 0.0
Usage: if a topological action improves the objective function by x, and x is smaller than this parameter, the effectiveness of this topological action will be considered inconsequential, and it will not be retained by the search-tree.
The absolute-minimum-impact-threshold can therefore fill two purposes:
- do not retain in the optimal solution of the RAO remedial actions with a negligible impact
- speed up the computation by avoiding the few final depths which only slightly improve the solution.

relative-minimum-impact-threshold#

Expected value: numeric value, percentage defined between 0 and 1 (1 = 100%)
Default value: 0.0
Usage: behaves like absolute-minimum-impact-threshold, but the threshold here is defined as a coefficient of the objective function value of the previous depth. In depth (n+1), if a topological action improves the objective function by x, with x < solution(depth(n)) x relative-minimum-impact-threshold, it will not be retained by the search-tree.

skip-actions-far-from-most-limiting-element#

Expected value: true/false
Default value: false
Usage: whether the RAO should skip evaluating topological actions that are geographically far from the most limiting element at the time of the evaluation. Proximity is defined by the number of country boundaries separating the element from the topological action (see max-number-of-boundaries-for-skipping-actions).
Setting this to true allows you to speed up the search tree RAO, while keeping a good precision, since topological actions that are far from the most limiting element have almost no impact on the minimum margin.

max-number-of-boundaries-for-skipping-actions#

Expected value: integer (>= 0)
Default value: 2
Usage: the maximum number of country boundaries between the most limiting element and the topological actions that shall be evaluated. The most limiting element is defined as the element with the minimum margin at the time of this evaluation.
If the most limiting element has nodes in two countries, the smallest distance is considered.
If the value is set to zero, only topological actions in the same country as the most limiting element will be evaluated in the search-tree.
If the value is set to 1, topological actions from direct neighbors will also be considered, etc.
Note that the topology of the network is automatically deduced from the network file: countries sharing tie lines are considered direct neighbors; dangling lines are not considered linked (ie BE and DE are not considered neighbors, even though they share the Alegro line)

Second preventive RAO parameters#

These parameters (second-preventive-rao) tune the behaviour of the second preventive RAO.

execution-condition#

Expected value: one of the following:
- “DISABLED”
- “COST_INCREASE”
- “POSSIBLE_CURATIVE_IMPROVEMENT”
Default value: “DISABLED”
Usage: configures whether a 2nd preventive RAO should be run after the curative RAO.
Note: if there are automatons, and if a 2nd preventive RAO is run, then a 2nd automaton RAO is also run
- DISABLED: 2nd preventive RAO is not run
- COST_INCREASE: a 2nd preventive RAO is run if the RAO’s overall cost has increased after optimisation compared to before optimisation; for example due to a curative CNEC margin decreased in 1st preventive RAO and not reverted during curative RAO
- POSSIBLE_CURATIVE_IMPROVEMENT: a 2nd preventive RAO is run only if it is possible to improve a curative perimeter, i.e. if the curative RAO stop criterion on at least one contingency is not reached.
  This depends on the value of parameter curative-stop-criterion:
  - SECURE: 2nd preventive RAO is run if one curative perimeter is not secure after optimisation
  - PREVENTIVE_OBJECTIVE: 2nd preventive RAO is run if one curative perimeter reached an objective function value after optimisation that is worse than the preventive perimeter’s (decreased by curative-min-obj-improvement)
  - PREVENTIVE_OBJECTIVE_AND_SECURE: 2nd preventive RAO is run if one of the two conditions above is satisfied
  - MIN_OBJECTIVE: 2nd preventive RAO is always run, trying to improve the minimum margin even more

re-optimize-curative-range-actions#

Expected value: true/false
Default value: false
Usage:
- false: the 2nd preventive RAO will optimize only the preventive remedial actions, keeping all optimal curative remedial actions selected during the curative RAO.
- true: the 2nd preventive RAO will optimize preventive remedial actions and curative range actions, keeping only the optimal curative topological actions computed in the curative RAO.

hint-from-first-preventive-rao#

Expected value: true/false
Default value: false
Usage: if set to true, the RAO will use the optimal combination of network actions found in the first preventive RAO, as a predefined combination (“hint”) to test at the first search depth of the second preventive RAO. This way, if this combination is optimal in the 2nd preventive RAO as well, getting to the optimal solution will be much faster.

CNECs that should not be optimised#

These parameters (not-optimized-cnecs) allow the activation of region-specific features, that de-activate the optimisation of specific CNECs in specific conditions.

do-not-optimize-curative-cnecs-for-tsos-without-cras#

Expected value: true/false
Default value: false
Usage: if this parameter is set to true, the RAO will detect TSOs not sharing any curative remedial actions (in the CRAC). During the curative RAO, these TSOs’ CNECs will not be taken into account in the minimum margin objective function, unless the applied curative remedial actions decrease their margins (compared to their margins before applying any curative action).
If it is set to false, all CNECs are treated equally in the curative RAO.
This parameter has no effect on the preventive RAO.
This parameter should be set to true for CORE CC. This parameter is not compatible with do-not-optimize-cnec-secured-by-its-pst for technical reasons.

do-not-optimize-cnec-secured-by-its-pst#

Expected value: a map with string keys and values. The keys should represent critical network element IDs, and the values should represent PST network element IDs.
Default value: empty map
Usage: when a critical network element (identified by its PowSyBl ID) is associated to a PST (identified by its PowSyBl ID) in this parameter, CNECs defined on the critical element will not be taken into account in the minimum margin objective function, as long as they can be secured by the associated PST. In other words, they will only be taken into account if the PST has too few tap positions left to reduce the flow constraints on these CNECs.
This parameter affects both preventive and curative RAOs.
It is actually used for the SWE CC process. This parameter is not compatible with do-not-optimize-curative-cnecs-for-tsos-without-cras for technical reasons.

Load-flow and sensitivity computation parameters#

These parameters (load-flow-and-sensitivity-computation) configure the load-flow and sensitivity computations providers from inside the RAO.

load-flow-provider#

Expected value: String, should refer to a PowSyBl load flow provider implementation
Default value: “OpenLoadFlow” (see OpenLoadFlow)
Usage: the name of the load flow provider to use when a load flow is needed

sensitivity-provider#

Expected value: String, should refer to a PowSyBl sensitivity provider implementation
Default value: “OpenLoadFlow” (see OpenLoadFlow)
Usage: the name of the sensitivity provider to use in the RAO

sensitivity-failure-over-cost#

Expected value: numeric value, where the unit is that of the objective function
Default value: 10000.0
Usage: if the systematic sensitivity analysis fails (= diverged) due to a combination of remedial actions, its objective function assessment will be penalized by this value. In other words, the criterion for this combination of RA will be (e.g.) : minMargin - sensitivity-failure-over-cost.
If this parameter is strictly positive, the RAO will discriminate the combinations of RA for which the systematic analysis didn’t converge. The RAO might therefore put aside the solution with the best objective-function if it has lead to a sensitivity failure, and instead propose a solution whose objective-function is worse, but whose associated network is converging for all contingency scenarios.

sensitivity-parameters#

Expected value: SensitivityComputationParameters (PowSyBl configuration)
Default value: PowSyBl’s default value (it is generally a bad idea to keep the default value for this parameter)
Usage: sensitivity-parameters is the configuration of the PowSyBl sensitivity engine, which is used within OpenRAO. The underlying “load-flow-parameters” is also used whenever an explicit pure load-flow computation is needed.

Multi-threading parameters#

These parameters (multi-threading) allow you to run a RAO making the most out of your computation resources.

contingency-scenarios-in-parallel#

Expected value: integer
Default value: 1
Usage: number of contingency scenarios (auto + curative instants) to optimise in parallel.
This parameter should therefore not exceed the number of cores of the computer on which the computation is made.
Note that the more contingencies are optimised in parallel, the more RAM is required by the RAO, and that the performance of the RAO might significantly decrease on a machine with limited memory resources.

preventive-leaves-in-parallel#

Expected value: integer
Default value: 1
Usage: this parameter sets the number of combination of remedial actions that the search-tree will investigate in parallel during the preventive RAO.
It should therefore not exceed the number of cores of the computer on which the computation is made.
Note that the more leaves are optimised in parallel, the more RAM is required by the RAO, and that the performance of the RAO might significantly decrease on a machine with limited memory resources.

auto-leaves-in-parallel#

Expected value: integer
Default value: 1
Usage: this parameter sets the number of combination of remedial actions that the search-tree will investigate in parallel during the automaton RAO.
It is separated from preventive-leaves-in-parallel and curative-leaves-in-parallel because during the curative RAO we also have the option to parallelize the contingency scenarios, so a compromise should be found. It is generally best to set this parameter to 1 and to maximize contingency-scenarios-in-parallel. Besides, there are generally fewer available auto remedial action than curative remedial actions.

curative-leaves-in-parallel#

Expected value: integer
Default value: 1
Usage: this parameter sets the number of combination of remedial actions that the search-tree will investigate in parallel during the curative RAO.
It is separated from preventive-leaves-in-parallel because during the curative RAO we also have the option to parallelize the contingency scenarios, so a compromise should be found. It is generally best to set this parameter to 1 and to maximize contingency-scenarios-in-parallel.

Extensions#

The following extensions can be added to RaoParameters when needed, in order to activate specific RAO features.

Loop-flow extension#

Adding a LoopFlowParameters extension to RaoParameters will activate loop-flow constraints.
(The RAO will monitor the loop-flows on CNECs that have a LoopFlowThreshold extension.)
The following parameters tune these constraints.
See also: Modelling loop-flows and their virtual cost

acceptable-increase#

Expected value: numeric values, in MEGAWATT unit
Default value: 0.0 MW
Usage: the increase of the initial loop-flow that is allowed by the optimisation. That is to say, the optimisation bounds the loop-flow on CNECs by:
LFcnec ≤ max(MaxLFcnec , InitLFcnec + acceptableAugmentation)
With LFcnec the loop-flow on the CNEC after optimisation, MaxLFcnec is the CNEC loop-flow threshold, InitLFcnec the initial loop-flow on the cnec, and acceptableAugmentation the so-called “loop-flow-acceptable-augmentation” coefficient.
If this constraint cannot be respected and the loop-flow exceeds the aforementioned threshold, the objective function associated to this situation will be penalized (see also violation-cost)

ptdf-approximation#

Expected value: one of the following:
- “FIXED_PTDF”
- “UPDATE_PTDF_WITH_TOPO”
- “UPDATE_PTDF_WITH_TOPO_AND_PST”
Default value: “FIXED_PTDF”
Usage: defines the frequency at which the PTDFs will be updated for the loop-flow computation. This parameter enables to set the desired trade-off between the accuracy of the loop-flow computation, and the computation time of the RAO.
- FIXED_PTDF: the PTDFs are computed only once at the beginning of the RAO.
- UPDATE_PTDF_WITH_TOPO: the PTDFs are re-computed for each new combination of topological actions (i.e. for each new node of the search-tree).
- UPDATE_PTDF_WITH_TOPO_AND_PST: the PTDFs are re-computed for each new combination of topological action and for each new combination of PST taps (i.e. for each iteration of the linear optimisation).
  Note that this option is only relevant in AC-loadflow mode, as the UPDATE_PTDF_WITH_TOPO already maximizes accuracy in DC.

constraint-adjustment-coefficient#

Expected value: numeric values, in MEGAWATT unit
Default value: 0.0 MW
Usage: this parameter acts as a margin which tightens, in the linear optimisation problem of RAO, the bounds of the loop-flow constraints. It conceptually behaves as the coefficient cAdjustment from the constraint below:
abs(LoopFlow(cnec)) <= LoopFlowThreshold - cAdjustment
This parameter is a safety margin that can absorb some approximations made in the linear optimisation problem of the RAO (non-integer PSTs taps, flows approximated by sensitivity coefficients, etc.), and therefore increase the probability that the loop-flow constraints which are respected in the linear optimisation problem, remain respected once the loop-flows are re-computed without the linear approximations.

violation-cost#

Expected value: numeric values, unit = unit of the objective function per MEGAWATT
Default value: 10.0
Usage: this parameter is the cost of each excess of loop-flow. That is to say, if the loop-flows on one or several CNECs exceed the loop-flow threshold, a penalty will be added in the objective function of the RAO equal to:
violation-cost x sum{cnec} excess-loop-flow(cnec)

countries#

Expected value: array of country codes “XX”
Default value: all countries encountered
Usage: list of countries for which loop-flows should be limited accordingly to the specified constraints. If not present, all countries encountered in the input files will be considered. Note that a cross-border line will have its loop-flows monitored if at least one of its two sides is in a country from this list.
Example of this parameter : [ “BE”, “NL” ] if you want to monitor loop-flows in and out of Belgium and the Netherlands.

MNEC extension#

Adding a MnecParameters extension to RaoParameters will activate MNEC constraints.
(The RAO will only monitor CNECs that are only “monitored”). The following parameters tune these constraints.
See also: Modelling MNECs and their virtual cost

acceptable-margin-decrease#

Expected value: numeric values, in MEGAWATT unit
Default value: 50 MW (required by CORE CC methodology)
Usage: the decrease of the initial margin that is allowed by the optimisation on MNECs.
In other words, it defines the bounds for the margins on the MNECs by
Mcnec ≥ max(0, m0cnec − acceptableDiminution)
With Mcnec the margin on the cnec after optimisation, m0cnec the initial margin on the cnec, and acceptableDiminution the so-called “acceptable-margin-decrease” coefficient.
For the CORE CC calculation, the ACER methodology fixes this coefficient at 50 MW.
For CSE CC calculation, setting this parameter to -99999 allows the MNEC constraints to consider the thresholds in the CRAC only.

violation-cost#

Expected value: numeric values, no unit (it applies as a multiplier for the constraint violation inside the objective function)
Default value: 10.0 (same as loop-flow violation cost)
Usage: the penalty cost associated to the violation of a MNEC constraint. In order to avoid optimisation infeasibility, the MNEC constraints are soft: they can be violated. These violations are penalized by a significant cost, in order to guide the optimiser towards a solution where - if possible - all MNECs’ constraints are respected. The penalty injected in the objective function is equal to the violation (difference between actual margin and least acceptable margin) multiplied by this parameter.

constraint-adjustment-coefficient#

Expected value: numeric values, in MEGAWATT unit
Default value: 0.0
Usage: this coefficient is here to mitigate the approximation made by the linear optimisation (approximation = use of sensitivities to linearize the flows, rounding of the PST taps).
Mcnec ≥ max(0 , m0cnec - acceptableDiminution) + constraintAdjustment
With constraintAdjustment the so-called “constraint-adjustment-coefficient”.
It tightens the MNEC constraint, in order to take some margin for that constraint to stay respected once the approximations are removed (i.e. taps have been rounded and real flow calculated)

Relative margins extension#

Adding a RelativeMarginsParameters extension is mandatory when objective function is relative.
See also: Modelling the maximum minimum relative margin objective function

ptdf-boundaries#

Expected value: array of zone-to-zone PTDF computation definition, expressed as an equation.
Zones are defined by their 2-character code or their 16-character EICode, inside { } characters.
Zones are seperated by + or -.
All combinations are allowed: country codes, EIC, a mix.
Default value: empty array
Usage: contains the boundaries on which the PTDF absolute sums should be computed (and added to the denominator of the relative RAM).
For example, in the SWE case, it should be equal to [ “{FR}-{ES}”, “{ES}-{PT}” ].
For CORE, we should use all the CORE region boundaries (all countries seperated by a - sign) plus Alegro’s special equation: “{BE}-{22Y201903144—9}-{DE}+{22Y201903145—4}”

ptdf-approximation#

Expected value: one of the following:
- “FIXED_PTDF”
- “UPDATE_PTDF_WITH_TOPO”
- “UPDATE_PTDF_WITH_TOPO_AND_PST”
Default value: “FIXED_PTDF”
Usage: defines the frequency at which the PTDFs will be updated for the relative margins computation. This parameter enables to set the desired trade-off between the accuracy of the relative margins computation, and the computation time of the RAO.
- FIXED_PTDF: the PTDFs are computed only once at the beginning of the RAO.
- UPDATE_PTDF_WITH_TOPO: the PTDFs are re-computed for each new combination of topological actions (i.e. for each new node of the search-tree).
- UPDATE_PTDF_WITH_TOPO_AND_PST: the PTDFs are re-computed for each new combination of topological action and for each new combination of PST taps (i.e. for each iteration of the linear optimisation).
  Note that this option is only relevant in AC-loadflow mode, as the UPDATE_PTDF_WITH_TOPO already maximizes accuracy in DC.

ptdf-sum-lower-bound#

Expected value: numeric value, no unit (homogeneous to PTDFs)
Default value: 0.01
Usage: PTDF absolute sums are used as a denominator in the objective function. In order to prevent the objective function from diverging to infinity (resulting in unbounded problems), the denominator should be prevented from getting close to zero. This parameter acts as a lower bound to the denominator.

Examples#

⚠️ NOTE
The following examples in json and yaml are not equivalent

{
  "version" : "2.4",
  "objective-function" : {
    "type" : "MAX_MIN_RELATIVE_MARGIN_IN_AMPERE",
    "forbid-cost-increase" : false,
    "curative-min-obj-improvement" : 0.0,
    "preventive-stop-criterion" : "SECURE",
    "curative-stop-criterion" : "PREVENTIVE_OBJECTIVE",
    "optimize-curative-if-preventive-unsecure" : true
  },
  "range-actions-optimization" : {
    "max-mip-iterations" : 5,
    "pst-penalty-cost" : 0.01,
    "pst-sensitivity-threshold" : 0.0,
    "pst-model" : "APPROXIMATED_INTEGERS",
    "hvdc-penalty-cost" : 0.001,
    "hvdc-sensitivity-threshold" : 0.0,
    "injection-ra-penalty-cost" : 0.001,
    "injection-ra-sensitivity-threshold" : 0.0,
    "linear-optimization-solver" : {
      "solver" : "CBC",
      "relative-mip-gap" : 0.001,
      "solver-specific-parameters" : "THREADS 10 MAXTIME 3000"
    }
  },
  "topological-actions-optimization" : {
    "max-preventive-search-tree-depth" : 2,
    "max-auto-search-tree-depth" : 1,
    "max-curative-search-tree-depth" : 2,
    "predefined-combinations" : [ "na1 + na2", "na4 + na5 + na6"],
    "relative-minimum-impact-threshold" : 0.0,
    "absolute-minimum-impact-threshold" : 1.0,
    "skip-actions-far-from-most-limiting-element" : false,
    "max-number-of-boundaries-for-skipping-actions" : 2
  },
  "multi-threading" : {
    "contingency-scenarios-in-parallel" : 4,
    "preventive-leaves-in-parallel" : 4,
    "curative-leaves-in-parallel" : 1
  },
  "second-preventive-rao" : {
    "execution-condition" : "POSSIBLE_CURATIVE_IMPROVEMENT",
    "re-optimize-curative-range-actions" : false,
    "hint-from-first-preventive-rao" : true
  },
  "not-optimized-cnecs" : {
    "do-not-optimize-curative-cnecs-for-tsos-without-cras" : false,
    "do-not-optimize-cnec-secured-by-its-pst" : {
      "NE1" : "PST1",
      "NE2" : "PST2"
    }
  },
  "load-flow-and-sensitivity-computation" : {
    "load-flow-provider" : "OpenLoadFlow",
    "sensitivity-provider" : "OpenLoadFlow",
    "sensitivity-failure-over-cost" : 0.0,
    "sensitivity-parameters" : {
      "version" : "1.0",
      "load-flow-parameters" : {
        "version" : "1.9",
        "voltageInitMode" : "DC_VALUES",
        "transformerVoltageControlOn" : false,
        "phaseShifterRegulationOn" : true,
        "noGeneratorReactiveLimits" : false,
        "twtSplitShuntAdmittance" : false,
        "shuntCompensatorVoltageControlOn" : false,
        "readSlackBus" : true,
        "writeSlackBus" : false,
        "dc" : false,
        "distributedSlack" : true,
        "balanceType" : "PROPORTIONAL_TO_GENERATION_P",
        "dcUseTransformerRatio" : true,
        "countriesToBalance" : [ "TR", "BE", "SI", "CH", "AL", "ES", "SK", "BA", "RO", "PT", "DE", "AT", "FR", "CZ", "ME", "NL", "PL", "GR", "IT", "UA", "HU", "BG", "MK", "HR", "RS" ],
        "connectedComponentMode" : "MAIN",
        "hvdcAcEmulation" : true,
        "dcPowerFactor" : 1.0,
        "extensions" : {
          "open-load-flow-parameters" : {
            "plausibleActivePowerLimit" : 10000.0,
            "minPlausibleTargetVoltage" : 0.5,
            "maxPlausibleTargetVoltage" : 1.5, 
            "maxNewtonRaphsonIterations" : 100,
            "newtonRaphsonConvEpsPerEq" : 1.0E-3,
            "slackBusSelectionMode" : "MOST_MESHED",
            "slackBusesIds" : [ ],
            "throwsExceptionInCaseOfSlackDistributionFailure" : false,
            "lowImpedanceBranchMode" : "REPLACE_BY_ZERO_IMPEDANCE_LINE",
            "loadPowerFactorConstant" : false,
            "addRatioToLinesWithDifferentNominalVoltageAtBothEnds" : true,
            "slackBusPMaxMismatch" : 1.0,
            "voltagePerReactivePowerControl" : false,
            "voltageInitModeOverride" : "NONE",
            "transformerVoltageControlMode" : "WITH_GENERATOR_VOLTAGE_CONTROL",
            "minRealisticVoltage" : 0.5,
            "maxRealisticVoltage" : 1.5,
            "reactiveRangeCheckMode" : "MAX"
          }
        }
      }
    }
  },
  "extensions" : {
    "loop-flow-parameters" : {
      "acceptable-increase" : 10.0,
      "ptdf-approximation" : "FIXED_PTDF",
      "constraint-adjustment-coefficient" : 10.0,
      "violation-cost" : 10.0,
      "countries" : [ "FR", "ES", "PT" ]
    },
    "mnec-parameters" : {
      "acceptable-margin-decrease" : 50.0,
      "violation-cost" : 10.0,
      "constraint-adjustment-coefficient" : 1.0
    },
    "relative-margins-parameters" : {
      "ptdf-boundaries" : [ "{FR}-{BE}", "{FR}-{DE}", "{BE}-{NL}", "{NL}-{DE}", "{DE}-{PL}", "{DE}-{CZ}", "{DE}-{AT}", "{PL}-{CZ}", "{PL}-{SK}", "{CZ}-{SK}", "{CZ}-{AT}", "{AT}-{HU}", "{AT}-{SI}", "{SI}-{HR}", "{SK}-{HU}", "{HU}-{RO}", "{HU}-{HR}", "{BE}-{22Y201903144---9}-{DE}+{22Y201903145---4}" ],
      "ptdf-approximation" : "FIXED_PTDF",
      "ptdf-sum-lower-bound" : 0.01
    }
  }
}

Based on PowSyBl’s configuration mechanism.

rao-objective-function:
  type: MAX_MIN_MARGIN_IN_AMPERE
  preventive-stop-criterion: SECURE
  curative-stop-criterion: SECURE

rao-range-actions-optimization:
  max-mip-iterations: 5
  pst-penalty-cost: 0.01
  pst-sensitivity-threshold: 0.01
  pst-model: APPROXIMATED_INTEGERS

rao-linear-optimization-solver:
  solver: CBC

rao-topological-actions-optimization:
  max-preventive-search-tree-depth: 3
  max-auto-search-tree-depth: 2
  max-curative-search-tree-depth: 3
  predefined-combinations: [ "{na1}+{na2}", "{na3}+{na4}+{na5}" ]
  relative-minimum-impact-threshold: 0.0
  absolute-minimum-impact-threshold: 2.0

rao-multi-threading:
  contingency-scenarios-in-parallel: 4
  preventive-leaves-in-parallel: 4
  curative-leaves-in-parallel: 1

rao-second-preventive-rao:
  execution-condition: POSSIBLE_CURATIVE_IMPROVEMENT
  re-optimize-curative-range-actions: true
  hint-from-first-preventive-rao: true

rao-not-optimized-cnecs:
  do-not-optimize-curative-cnecs-for-tsos-without-cras: false

rao-load-flow-and-sensitivity-computation:
  load-flow-provider: OpenLoadFlow
  sensitivity-provider: OpenLoadFlow

load-flow-default-parameters:
  voltageInitMode: DC_VALUES
  balanceType: PROPORTIONAL_TO_GENERATION_P
  countriesToBalance: AL,AT,BA,BE,BG,CH,CZ,DE,ES,FR,GR,HR,HU,IT,ME,MK,NL,PL,PT,RO,RS,SI,SK,UA
  update parameters to version 2.0 phaseShifterRegulationOn: true

open-loadflow-default-parameters:
  minPlausibleTargetVoltage: 0.5
  maxPlausibleTargetVoltage: 1.5
  plausibleActivePowerLimit: 10000
  newtonRaphsonConvEpsPerEq : 1.0E-2